I thought this was a pretty interesting problem that I couldn’t solve in the actual time span, so I wanted to solve it afterwards (after many attempts of failed trig bashing…)

Problem Statement

An equilateral triangle is a triangle in which all three sides are the same length. An equilateral triangle is also equiangular, meaning that all three interior angles are congruent and each 60 degrees. For example, if the points (7, -6) and (1, 2) are given, two equilateral triangles can be formed. The first triangle (dashed lines) is formed with addition of the point A (-2.93, -7.2), and the second triangle (dotted lines) is formed with the addition of the point B (10.93, 3.2). Note: these values are rounded to two decimal places.

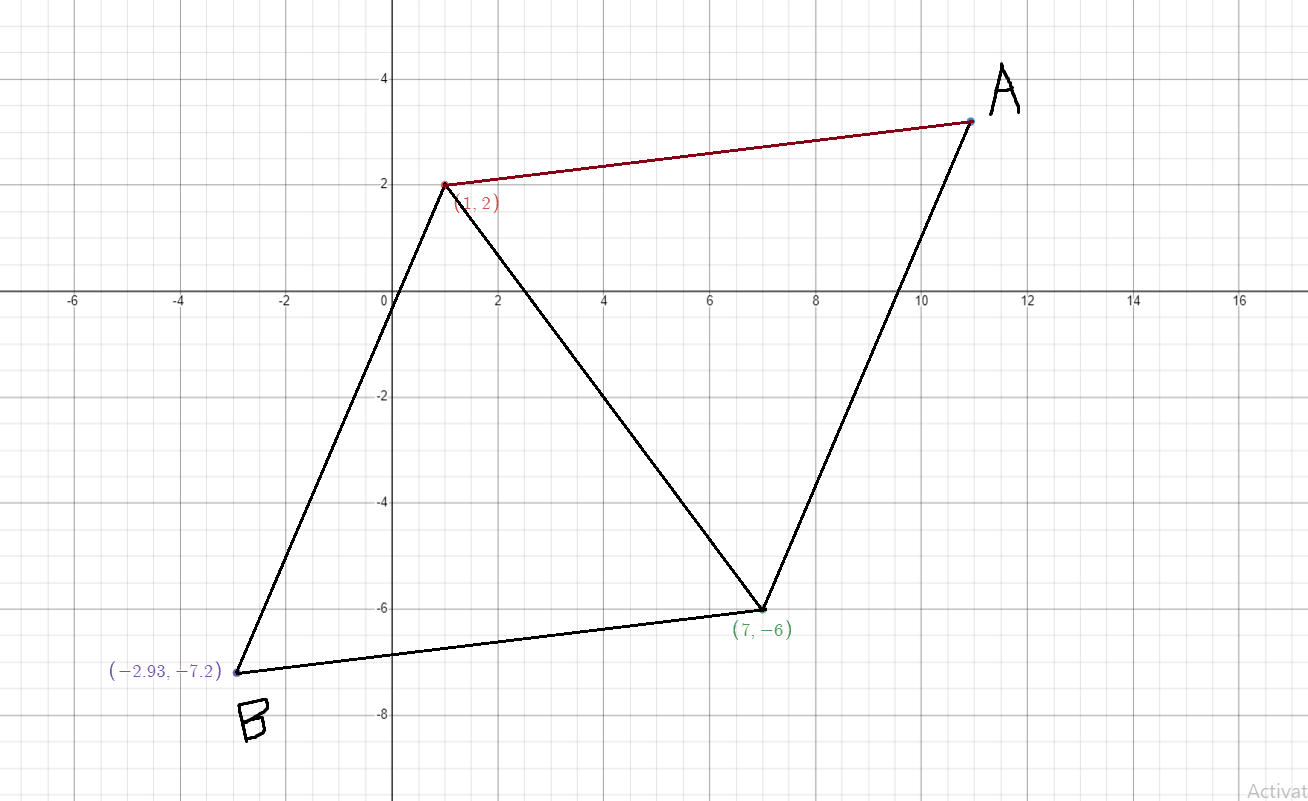
A beautiful recreation of the given example

Dominika has been given two coordinates representing two out of the three points on an equilateral triangle, but the third point is missing. Can you help Dominika write a program that is able to find these two missing points?

Input: First line will contain an integer N in range [1, 20], the number of test cases. Each of the following N lines will contain four whole numbers, seperated by spaces. These numbers represent

$$X_1, Y_1, X_2, Y_2$$

where A and B are the two given points. All whole numbers will be in range [-20, 20]

Output: For each test case you are to output: "Test case: #" where # is the current test case, followed by the two points that are missing, that are needed to make the two equilateral triangles. Each point is to be printed out on its own, individual line. The output should be rounded and printed out to two decimal places. The point with the smallest x value should be output first. If the x coordinates are the same, then output the point with the smallest value.